
সক্রেটিস বলেছিলেন, “আমি শুধু একটা জিনিসই জানি। সেটা হচ্ছে আমি কিছুই জানি না।” এর অর্থ সক্রেটিস কি আসলেই কিছু জানেন না, নাকি একটা জিনিস, বা অনেক জিনিসই জানেন?
সক্রেটিসের এই বাক্যটি একটি প্যারাডক্স। প্যারাডক্স হচ্ছে সে ধরনের বাক্য বা উক্তি, যা থেকে অনন্য কোনো সিদ্ধান্তে আসা যায় না। বরং এ ধরনের সমস্যার বিবরণগুলো দুটি পরস্পরবিরোধী সমাধান তৈরি করে, যার একটি সত্য হলে অন্যটি সম্ভব না। কিছু প্যারাডক্স আছে যাদের কোনো সমাধান নেই, আবার কিছু আছে যাদের অত্যন্ত জটিল গাণিতিক এক দার্শনিক সমাধান আছে। কিন্তু সমাধান নয়, চলুন জেনে নিই এরকম কিছু বিখ্যাত প্যারাডক্সের কথা।
একিলিস এবং কচ্ছপের দৌড় প্রতিযোগিতা
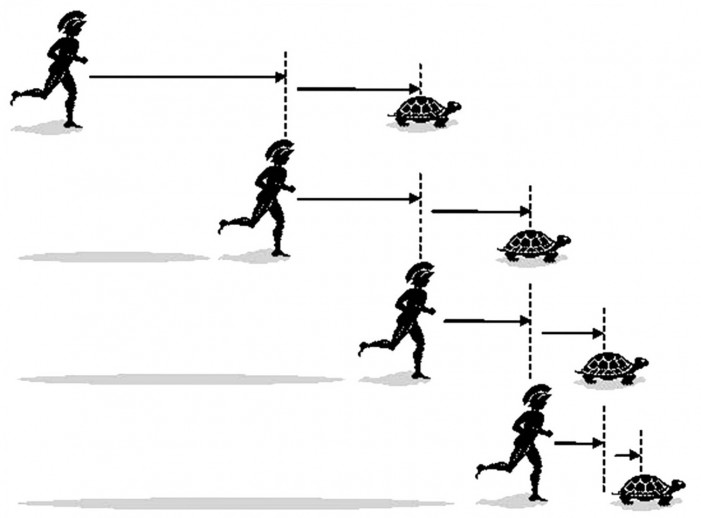
একিলিস ও কচ্ছপের দৌড় প্রতিযোগিতা; Source: ibmathsresources.com
খ্রিস্টপূর্ব পঞ্চম শতকে গ্রীক দার্শনিক জেনো গতি সম্পর্কিত কয়েকটি জটিল প্যারাডক্স তৈরি করে গেছেন। একিলিস এবং কচ্ছপের দৌড় প্রতিযোগিতা হচ্ছে সেগুলোর মধ্যে একটি। ধরা যাক, গ্রীক বীর একিলিসের সাথে একটি দৌড় প্রতিযোগিতা অনুষ্ঠিত হবে। যেহেতু একিলিস দ্রুত দৌড়াতে পারে, তাই কচ্ছপের প্রতি যেন অবিচার না হয়, সেজন্য সিদ্ধান্ত নেওয়া হয় কচ্ছপকে কিছুটা সামনে থেকে দৌড় শুরু করার সুযোগ দেওয়া হবে। ধরা যাক, কচ্ছপ একিলিসের চেয়ে ৫০০ মিটার সামনে থেকে দৌড় করল।
এখন প্রতিযোগিতা শুরু হওয়ার সাথে সাথেই একিলিস অত্যন্ত দ্রুতগতিতে এই ৫০০ মিটার অতিক্রম করে কচ্ছপের পূর্বের স্থানে চলে আসবে। কিন্তু ততক্ষণে কচ্ছপ তার স্বাভাবিক ধীর গতিতে কিছুটা হলেও দূরত্ব অতিক্রম করবে। মনে করা যাক, কচ্ছপ এই সময়ে মাত্র ৫০ মিটার পথ অতিক্রম করল। এই ৫০ মিটার পথ অতিক্রম করতে একিলিসের আরও কম সময় লাগবে। কিন্তু ততক্ষণে কচ্ছপ আরো ৫ মিটার এগিয়ে যাবে।
এই প্রক্রিয়া চলতেই থাকবে এবং একিলিস যতোই কচ্ছপের অবব্যহিত পূর্বের আসার পূর্বেই কচ্ছপ অতিক্ষুদ্র দূরত্ব হলেও অতিক্রম করবে। অর্থাৎ জেনোর প্রস্তাব অনুযায়ী একিলিসের পক্ষে কখনোই কচ্ছপকে ছাড়িয়ে সামনে যাওয়া সম্ভব হবে না। অথচ বাস্তব জীবনে আমরা প্রতিনিয়তই এরকম ক্ষেত্রে যেকোনো দৌড়বিদ অথবা গাড়িকে পেছন থেকে এসে অন্য দৌড়বিদ বা গাড়িকে অতিক্রম করতে দেখি।
থিসিয়াসের জাহাজ
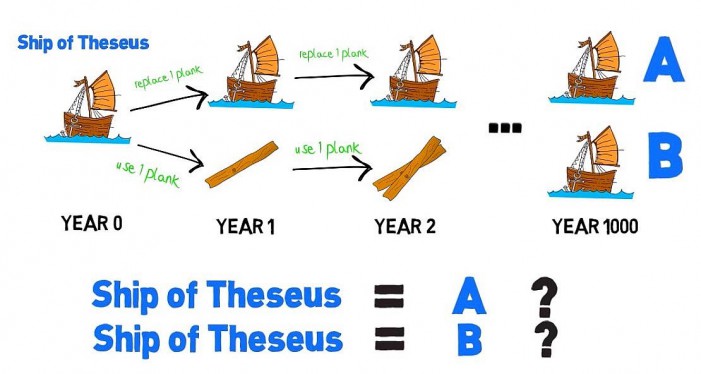
থিসিয়াসের জাহাজ প্যারাডক্স; Source: onedio.com
এটিও একটি প্রাচীন গ্রীক প্যারাডক্স। যদিও প্লেটো এবং হেরাক্লিটাসও এই সমস্যাটি নিয়ে আলোচনা করেছিলেন, কিন্তু এর সবচেয়ে বিখ্যাত বর্ণনাটি পাওয়া যায় গ্রীক জীবনীকার প্লুটার্কের রচনায়। তিনি সমস্যাটিকে বর্ণনা করেন এভাবে, প্রাচীন গ্রীসের পৌরাণিক রাজা থিসিয়াস যে জাহাজে চড়ে ক্রীট থেকে ফেরত এসেছিলেন, তা এথেন্সবাসীরা সংরক্ষণ করে রেখেছিল। কিন্তু দীর্ঘদিন পরে জাহাজটির লগি, বৈঠা, পাটাতন প্রভৃতি নষ্ট হয়ে যেতে শুরু করলে তারা সেগুলো নতুন কাঠের গুঁড়ি দ্বারা প্রতিস্থাপন করতে শুরু করেন। ধীরে ধীরে জাহাজটির কাঠামোর অধিকাংশই প্রতিস্থাপিত হয়ে যায়। প্লুটার্ক প্রশ্ন করেন, এখন জাহাজটি কি আগের জাহাজই আছে, নাকি এটি নতুন একটি জাহাজ?
এই সমস্যাটির ভিন্ন ভিন্ন রূপও আছে। একটি বর্ণনায় বলা হয়, একটি কুড়ালের মাথা এবং হাতল দুটোই যদি পরিবর্তন করা হয়, তাহলে কি সেটি পূর্বের কুড়ালই থাকে, নাকি নতুন কুড়ালে পরিণত হয়? আরেকটি বর্ণনায় কল্পনা করা হয়, একটি মোজার মধ্যে ছিদ্র তৈরি হওয়ার পর তাতে তালি দিয়ে ঠিক করা হলো। দ্বিতীয় আরেকটি ছিদ্র তৈরি হওয়ার পর সেখানেও তালি দেওয়া হলো। এভাবে কতগুলো তালি দেওয়ার পরেও বলা যাবে যে, মোজাটি আগের মোজাই আছে?
গ্র্যান্ডফাদার প্যারাডক্স
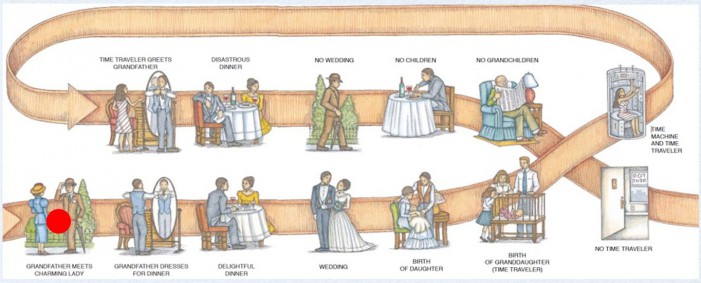
গ্র্যান্ডফাদার প্যারাডক্স; Source: physicsandquantummechanics.com
টাইম ট্রাভেল বা সময় পরিভ্রমণ কল্পবিজ্ঞানের একটি জনপ্রিয় অংশ। কিন্তু সময় পরিভ্রমণ যদি সম্ভব হতো, তাহলে বিভিন্ন ধরনের জটিলতা সৃষ্টি হতো। সময় পরিভ্রমণ সংক্রান্ত একাধিক প্যারাডক্স আছে, যার মধ্যে সবচেয়ে বিখ্যাত হচ্ছে গ্র্যান্ডফাদার প্যারাডক্স। এতে বলা হয়, যদি কেউ টাইম ট্রাভেল করে নিজের অতীতে ফিরে গিয়ে বাবার জন্মের আগেই দাদাকে হত্যা করে ফেলে, তাহলে তার নিজের অস্তিত্বই থাকার কথা না। গ্র্যান্ডফাদার প্যারাডক্স দ্বারা মূলত এই ধারণাটিই বোঝানো হয় যে, অতীতে ফিরে গিয়ে যেকোনো ক্ষুদ্র পরিবর্তন ঘটালে বর্তমান পৃথিবীতে তার যে বিশাল প্রভাব পড়বে, তা পরস্পরের সাথে সামঞ্জস্যপূর্ণ না।
গ্র্যান্ডফাদার প্যারাডক্সেরও অনেকগুলো ভিন্ন ভিন্ন রূপ আছে। তার মধ্যে একটি হচ্ছে হিটলারকে হত্যা করার প্যারাডক্স। অনেকেই বলে টাইম ট্রাভেল সম্ভব হলে প্রথমেই হিটলারের শিশুকালে গিয়ে তাকে হত্যা করে ফেলা উচিত, যেন সে দ্বিতীয় বিশ্বযুদ্ধ শুরু করতে না পারে। কিন্তু এটা সম্ভব না। কারণ হিটলারকে যদি আগেই হত্যা করে ফেলা হয়, তাহলে তার পরবর্তী প্রজন্মের মানুষের হিটলার সম্পর্কে কোনো ধারণাই থাকবে না, ফলে তাকে হত্যা করার জন্য কেউ অতীতে ফিরে যেতে চাইবে না।
বুটস্ট্র্যাপ প্যারাডক্স

বুটস্ট্র্যাপ প্যারাডক্স; Source: imgfave.com
বুটস্ট্র্যাপ প্যারাডক্সও টাইম ট্রাভেল সংক্রান্ত প্যারাডক্স, কিন্তু এটি গ্র্যান্ডফাদার প্যারাডক্সের বিপরীত। এতে অতীতে গিয়ে কোনো ঘটনার পরিবর্তন করা হয় না, বরং ভবিষ্যত থেকে কোনো তথ্য অতীতে নিয়ে আসা হয়, যা পরবর্তীতে কাজে লাগানো হয়। তখন প্রশ্ন ওঠে, তথ্যটি আসলে কোথা থেকে এসেছে।
উদাহরণস্বরূপ ধরা যায়, কেউ দোকান থেকে রবীন্দ্রনাথ ঠাকুরের গীতাঞ্জলী ক্রয় করে টাইম ট্রাভেল করে যুবক বয়সের রবীন্দ্রনাথ ঠাকুরকে দিয়ে এলো। এরপর রবীন্দ্রনাথ ঠাকুর সেটা দেখে দেখে গীতাঞ্জলীর অনুলিপি তৈরি করলেন, যা পরবর্তী বিখ্যাত হয়ে যাওয়ার ফলে দোকানটিতে স্থান পেল। কিন্তু তাহলে গীতাঞ্জলীর আসল লেখক কে?
বুটস্ট্র্যাপ শব্দটির অর্থ জুতার ফিতা। ইংরেজি প্রবাদ ‘Pulling yourself by bootstrap‘ তথা নিজের জুতার ফিতা ধরে নিজেকে টেনে তোলা থেকেই এর এই নামকরণ করা হয়েছে।
গ্রেলিং-নেলসন প্যারাডক্স

হেটেরোলজিক্যাল ওয়ার্ড প্যারাডক্স; Source: Redbubble
যেকোনো ভাষার গুণবাচক শব্দগুলোকে অর্থগত দিক থেকে দুই ভাগে ভাগ করা যায়। অটোলজিকাল (Autological) শব্দ হচ্ছে সে ধরনের শব্দ, যেগুলো নিজেকেই বর্ণনা করে। যেমন ‘Noun‘ শব্দটি নিজেই Noun, ‘English‘ শব্দটি নিজেই ইংলিশ বা ইংরেজি ভাষার শব্দ, ‘Unhyphenated‘ শব্দটিতে কোনো হাইফেন নেই, তাই এই শব্দগুলো অটোলজিক্যাল। অন্যদিকে হেটেরোলজিক্যাল (Heterological) শব্দ হচ্ছে সে ধরনের শব্দ, যেগুলো নিজেকে বর্ণনা করে না। যেমন ‘Long‘ শব্দটি আসছে ছোট, ‘Hyphenated‘ শব্দটিতে কোনো হাইফেন নেই, ‘Verb‘ শব্দটি আসলে ক্রিয়াপদ না। কাজেই এরা সকলে হেটেরোলজিক্যাল শব্দ।
১৯০৮ সালে কার্ট গ্রেলিং এবং লিওনার্ড নেলসন প্রশ্ন উত্থাপন করেন যে, ‘Heterological‘ শব্দটি নিজে কি হেটেরোলজিক্যাল? যদি উত্তর না হয়, তার অর্থ এটি অটোলজিক্যাল, অর্থাৎ এটি নিজেকে বর্ণনা করবে, অর্থাৎ হেটেরোলজিক্যাল শব্দটি হেটেরোলজিক্যাল হবে, কিন্তু তার অর্থ এটি নিজেকে বর্ণনা করবে না, যা পরস্পরবিরোধী। আবার উত্তর যদি হ্যাঁ হয়, তাহলেও হেটেরোলজিক্যাল শব্দটি হেটেরোলজিক্যাল হবে, অর্থাৎ এটি নিজেকে বর্ণনা করবে না, যার অর্থ এটি হেটেরোলজিক্যাল না। এটাও পরস্পরবিরোধী।
সর্বশক্তিমান সত্ত্বার প্যারাডক্স

ওমনিপটেন্স প্যারাডক্স; Source: ctsportaldotorg.wordpress.com
ওমনিপটেন্স প্যারাডক্স (Omnipotence paradox) বা অসীম শক্তি প্যারাডক্স নামে পরিচিত এই সমস্যাটি দর্শন শাস্ত্রের একটি সুপরিচিত সমস্যা। বিভিন্নভাবে একে প্রকাশ করা যায়। তার মধ্যে সবচেয়ে সহজ এবং বহুল ব্যবহৃত রূপ হচ্ছে, যদি ধরে নেওয়া হয় অসীম ক্ষমতার অধিকারী কোনো সত্ত্বা, যেমন ঈশ্বর যেকোনো কিছু তৈরি করতে পারেন এবং যেকোনো ভারী বস্তু উত্তোলন করতে পারেন, তাহলে তিনি কি এমন ভারী কোনো পাথর তৈরি করতে পারবেন, যেটি কেউই উত্তোলন করতে পারবে না? এমনকি, তিনি নিজেও উত্তোলন করতে পারবেন না?
মিথ্যাবাদী প্যারাডক্স

মিথ্যাবাদী প্যারাডক্স; Source: propensityforcuriosity.com
এটা অনেকটা গ্রেলিং-নেলসন প্যারাডক্সের মতোই। কেউ যদি বলে “আমি মিথ্যা কথা বলছি“, তাহলে তার এই বাক্যটি কি সত্য না মিথ্যা? যদি তার বাক্যটি সত্য ধরে নেওয়া হয়, তার মানে সে মিথ্যা কথা কথা বলছে, অথচ ধরে নেওয়া হয়েছিল সে সত্য কথা বলছে। আবার যদি তার বাক্যটিকে মিথ্যা ধরা হয়, তাহলে তার মিথ্যা বলার দাবিটা মিথ্যা, অর্থাৎ সে সত্য কথা বলছে, কিন্তু ধরে নেওয়া হয়েছিল সে মিথ্যা কথা বলছে। উভয় ক্ষেত্রেই সমাধানগুলো পরস্পর বিরোধী।
ইন্টারেস্টিং নাম্বার প্যারাডক্স
১ হচ্ছে প্রথম স্বাভাবিক পূর্ণ সংখ্যা, ২ হচ্ছে প্রথম মৌলিক সংখ্যা, ৩ হচ্ছে প্রথম বেজোড় মৌলিক সংখ্যা- এভাবে বিভিন্ন সংখ্যার কিছু না কিছু অনন্য বৈশিষ্ট্য পাওয়া যায়। বলা হয়, প্রথম যে সংখ্যাটি পাওয়া যাবে, যার কোনো বিশেষ বৈশিষ্ট্য নেই, সেটি হবে একটি বিশেষত্বহীন বা ‘আন-ইন্টারেস্টিং’ সংখ্যা। কিন্তু এই প্যারাডক্স অনুযায়ী, কোনো বিশেষত্ব না থাকাই একটি বিশেষ বৈশিষ্ট্য। কাজেই এই সংখ্যাটিও ‘আন-ইন্টারেস্টিং’ হতে পারে না। এভাবে দেখানো যায়, কোনো সংখ্যাই আসলে ‘আন-ইন্টারেস্টিং’ হতে পারবে না।
অপ্রত্যাশিত ফাঁসি প্যারাডক্স

অপ্রত্যাশিত ফাঁসি প্যারাডক্স; Source: affordablehousinginstitute.org
এই প্যারাডক্সটি এরকম যে, বিচারক আসামীর মৃত্যুদন্ড দিয়ে বললেন, তার ফাঁসি হবে আগামী এক সপ্তাহের মধ্যে যেকোনো দিন। কিন্তু সেটি এমন একদিন হবে যে, তা আসামীর কাছে অপ্রত্যাশিত বা চমক হিসেবে থাকবে। আসামী চিন্তা করে দেখল, যদি চমক হয়, তাহলে ৭ম দিনে তার ফাঁসি হতে পারবে না। কারণ প্রথম ৬ দিনে যদি তার ফাঁসি না হয়, তাহলে ৬ষ্ঠ দিনেই সে বুঝে যাবে যে, পরদিন তার ফাঁসি, কাজেই সেটা আর চমক থাকবে না। একই যুক্তিতে ৬ষ্ঠ, ৫ম, কোনো দিনই তার ফাঁসি হবে না। কিন্তু সমস্যাটা হবে, যদি আসামী নিশ্চিত হয়ে যায় যে, বিচারকের শর্ত অনুযায়ী তার ফাঁসি হওয়া সম্ভব না, তখন যেকোনো দিন হঠাৎ করে তার ফাঁসি দিলে সেটাই তার কাছে চমক বলে মনে হবে এবং বিচারকের অঙ্গীকারও পূরণ হবে।
পুত্র-কন্যা প্যারাডক্স
এটি একটি সম্ভাব্যতা বিষয়ক প্যারাডক্স। এতে বলা হয়, কোনো পরিবারের দুটি সন্তান আছে। তাদের মধ্যে একটি পুত্র সন্তান। কতটুুকু সম্ভাবনা আছে যে, দুটি সন্তানই পুত্র? স্বাভাবিক ভাবে চিন্তা করলে মনে হয়, যেহেতু অপর সন্তানটি কেবলমাত্র পুত্র অথবা কন্যা হতে পারে, তাই উত্তরটি হবে ১/২।
কিন্তু অন্যভাবে চিন্তা করলে দেখা যায়, একটি পরিবারের দুই সন্তানের চার রকম সমন্বয় সম্ভব: পুত্র-পুত্র, পুত্র-কন্যা, কন্যা-পুত্র এবং কন্যা-কন্যা। এক্ষেত্রে যেহেতু জানা আছে একটি সন্তান পুত্র, তাই কন্যা-কন্যা সম্ভাবনাটি বাদ যাবে এবং বাকি তিনটি সমন্বয় থেকে যেকোনোটিই সম্ভব হতে পারে। অর্থাৎ এক্ষেত্রে উত্তর হবে ১/৩।
ফিচার ইমেজ- Steemit








