
৭
ইউরোপে রকেট প্রযুক্তি মঙ্গোলীয়দের হাত ধরে সেই ১৩ শতকের দিকেই চলে এসেছিল। ১৫ শতকের দিকে এসে এই প্রযুক্তির কিছুটা উন্নতিও হয়েছে। তারপর, এ নিয়ে দীর্ঘদিন ইউরোপে আর কিছু হয়নি। এসব অবশ্য আমরা আগেই দেখেছি।
১৯ শতকের দিকে এসে উইলিয়াম কনগ্রেভের হাত ধরে রকেট প্রযুক্তি আবার উন্নতির মুখ দেখল। কথা হলো, কে এই উইলিয়াম কনগ্রেভ?

উইলিয়াম কনগ্রেভের বাবার নামও ছিল উইলিয়াম কনগ্রেভ! তার বাবাকে বলা হয় ১ম ব্যারনেট। সেই হিসেবে আমাদের কনগ্রেভ হলেন দ্বিতীয় ব্যারনেট। ব্রিটিশ রাজ-অস্ত্রশালার তদারকির দায়ত্বে ছিলেন তার বাবা। স্বাভাবিকভাবেই রকেট নিয়ে কনগ্রেভের (২য় ব্যারনেট) মধ্যে কিছুটা আগ্রহ তৈরি হয়েছিল। সেই আগ্রহ হালে পানি পাওয়ার জন্য মাঝে সাঝে টুকটাক নানা ধরনের এক্সপেরিমেন্ট করারও সুযোগ পেয়েছিলেন তিনি।
১৭৯৯ সালে মহীশুরের রকেট হাতে পাওয়ার পরে নবোদ্যমে কাজে নামেন কনগ্রেভ। মহীশুরের রকেট দেখে তিনি বুঝেছিলেন, ধাতব জ্বালানীকক্ষ ব্যবহার করতে হবে। কিন্তু শুধু জ্বালানী কক্ষই তো সব না। কিছু ব্যাপার আছে, যেগুলো সহসা সাধারণ মানুষের চোখে পড়তে চায় না। তবে একজন বিজ্ঞানীর চোখে এগুলোই আগে পড়বে। যেমন- পরিমাপ।

মানে, সবকিছুর একটা মাপজোখ থাকতে হবে। আর, মাপের হেরফেরের জন্য ফলাফল অবশ্যই ভিন্ন হবে। যেমন- রকেট কতটা ভারী, এর নাক কতটা চোখা-এগুলি খুবই গুরুত্বপূর্ণ। সবচেয়ে গুরুত্বপূর্ণ জ্বালানী ও এর উপাদানের পরিমাণ। কতটা জ্বালানীর জন্য রকেট কতটুকু দূরত্ব যাচ্ছে, জ্বালানী বাড়িয়ে দিলে এই দূরত্ব বাড়ছে নাকি কমছে, জ্বালানী মিশ্রণের উপাদানগুলোর কোনটার শতকরা হার কতটুকু হলে রকেটের পাল্লা, বেগ ইত্যাদি বেড়ে যাচ্ছে- এসব নিয়ে নানা ধরনের এক্সপেরিমেন্ট করলেন কনগ্রেভ।
এসব করতে গিয়ে ৩ পাউন্ড (১.৩ কেজির মতো) থেকে ৩২ পাউন্ড (১৪.৫ কেজির মতো) ভারী বিভিন্ন ধরনের রকেট বানিয়েছিলেন কনগ্রেভ। ৩২ পাউন্ডের এই রকেট প্রায় ৩,০০০ গজ দূরত্ব পাড়ি দিতে পারত। সেই সাথে নতুন ধরনের জ্বালানী মিশ্রণও বানিয়েছিলেন তিনি।
১৮০৪ সালে তার বানানো রকেট প্রথমবারের মতো পরীক্ষা করে দেখা হয়। তখনও অবশ্য ৩২ পাউন্ডের রকেটটি বানাননি তিনি। এরপর, ১৮০৫ সালে স্যার সিডনি স্মিথের নেতৃত্বে বুলন শহরের ওপরে রকেট হামলা করে ব্রিটিশরা। তবে খুব বেশি ক্ষয়ক্ষতি করতে পারেনি। পরের বছর ৩২ পাউন্ডের সেই রকেটটি বানান কনগ্রেভ। একই শহরের ওপরে আবারও রকেট হামলা করে ব্রিটিশরা। প্রচুর ক্ষয়ক্ষতিও হয়।
আসলে, এ সময় ব্রিটিশদের সাথে ফ্রান্সের সেই বিখ্যাত যুদ্ধ চলছিল। ‘সেই বিখ্যাত যুদ্ধ’ মানে ‘নেপোলিওনিক যুদ্ধ‘। ১৮০৫ সালে শুরু হওয়ার পরে কয়েক পর্বে এই যুদ্ধ চলতে থাকে। শেষ হয় এসে ওয়াটারলু যুদ্ধে। এই যুদ্ধের কথা ইতিহাসে আগ্রহী সবারই শোনার কথা। নেপোলিয়ন হেরে যাওয়ার মাধ্যমে এই সংঘাত শেষ হয়। আর, নেপোলিয়নকে পরাজিত করা ওয়েলিংটন হয়ে যান কিংবদন্তিতুল্য বীর।
এই যুদ্ধের সময়, ১৮০৭ সালে কোপেনহেগেনের ওপরে ৩০০ রকেট নিক্ষেপ করেছিল ব্রিটিশরা। ফলে, ধুলোয় মিশে যায় কোপেনহেগেন।

এখানে একটা গুরুত্বপূর্ণ কথা বলে নেওয়া দরকার। একটা আস্ত শহরকে লক্ষ্য করে রকেট ছুঁড়লে লক্ষ্যভেদের কোনো ব্যাপার আসলে থাকে না। তবে পরীক্ষা করে ব্রিটিশরা দেখেছিল, এই রকেটগুলো খুব ভালো লক্ষ্যভেদ করতে পারত না। অবশ্য, এগুলো বিস্ফোরিত হতো ভয়ংকরভাবে। আর, অস্ত্র হিসেবে নিখুঁত লক্ষ্যভেদের চেয়ে এই তীব্র বিস্ফোরণই তখন বেশি গুরুত্বপূর্ণ ছিল। এমনিতে রকেট যা ক্ষতি করত, প্রতিপক্ষের মানসিক ক্ষতি হতো আরো প্রবল। যুদ্ধজয়ের সবটুকু ইচ্ছেশক্তি গুঁড়িয়ে যাওয়ার মতো অবস্থা। স্বাভাবিক। শত্রু সামনে থাকলে তাকে ঠেকানো যায়। আকাশপথে উড়ে আসা এই শত্রুকে ঘোড়সওয়ার যোদ্ধারা থামাবে কীভাবে?

অদ্ভুত হলেও সত্যি, ওয়াটারলুর যুদ্ধে নেপোলিয়নের হারের পেছনে এই রকেট খুব গুরুত্বপূর্ণ কোনো ভূমিকা রাখেনি। বরং অনেক দূরে, ইন্দোনেশিয়াতে এক আগ্নেয়গিরির অগ্নুৎপাতের ফলে ওয়াটারলুর যুদ্ধের সময় আকাশ ফেটে বৃষ্টি নেমেছিল। এই বৃষ্টিই আসলে হারিয়ে দিয়েছিল নেপোলিয়নকে। [কীভাবে? সেই গল্পটা পড়তে পারবেন এখানে।]
একদিকে যখন অস্ত্র হিসেবে রকেট দিন দিন আরো ভয়ংকর হয়ে উঠছে, অন্যদিকে বিজ্ঞানের জগতে ততদিনে এক দারুণ বিপ্লব ঘটে গেছে। এই বিপ্লবের শুরুটা অবশ্য হয়েছিল আরো দু’শো বছর আগে। আর, এর মধ্যে দিয়ে যুদ্ধাস্ত্র রকেট পরিণত হতে চলেছে মহাকাশ জয়ের মূল উপাদানগুলোর একটিতে।
৮
এতদিন রকেট শুধুই যুদ্ধাস্ত্র হিসেবে ব্যবহৃত হয়েছে। কারণ, রকেট দিয়ে যে আর কিছু করা যেতে পারে, সেটা ভাবার মতো কেউ ছিলেন না। তাছাড়া এই ‘আর কিছু’ করার জন্য যে বিজ্ঞানের দরকার, সেটাও তখনো মানুষ জানত না।
১৬ শতক থেকে বিজ্ঞানের জগতে বিপ্লবের হাওয়া লাগল। কোপার্নিকাস, টাইকোব্রাহে ও গ্যালিলিও গ্যালিলির হাত ধরে আমরা জানলাম, পৃথিবী বা মানুষ মহাবিশ্বের কেন্দ্রে নেই। বরং সূর্যকে ঘিরে অন্যান্য গ্রহগুলোর মতো করেই ঘুরপাক খাচ্ছে।
এর কিছুদিন পরের কথা। ১৮ শতক শেষ করে মানুষের ইতিহাস ১৯ শতকে পা রেখেছে। এ সময় মঞ্চে এলেন নিউটন। মহাকর্ষ তত্ত্ব আবিষ্কার করলেন তিনি। বললেন, গ্রহ-নক্ষত্ররাও এই সূত্র মেনেই ছুটে চলেছে।
বিজ্ঞানের এই ইতিহাসটুকু প্রায় সবারই জানার কথা। তারপরও এ নিয়ে ঘটা করে বলার কারণ, নিউটন মোটামুটি একা হাতেই রকেট বিজ্ঞানের ভিত্তি গড়ে দিয়েছিলেন। তার সূত্রগুলো মানুষের মহাকাশ যাত্রার ইতিহাসে অসম্ভব গুরুত্বপূর্ণ ভূমিকা রেখেছে। এক মহাকর্ষ সূত্রের ওপরে ভর করে সুদূর চাঁদ থেকে ঘুরে এসেছেন নভোচারীরা। সূত্রটি আমরা সবাই জানি। F = Gmm’/r2। এতে দুটি বস্তুর ভর বসিয়ে হিসাব করার উপায়টাও শিক্ষার্থীদের জানার কথা। আমাদের দেশের অষ্টম শ্রেণীতেই এটি পড়ানো হয়। সূত্র অনুযায়ী মহাকর্ষ যেহেতু দূরত্বের বর্গের ব্যস্তানুপাতিক হারে কাজ করে, তাই একে ‘ব্যস্তানুপাতিক সূত্র’ও বলা হয়। কিন্তু এর ভৌত গুরুত্ব নিয়ে আমরা আসলে সেভাবে ভাবি না। কিন্তু এ নিয়ে ভাবা দরকার। কারণটা তো আগেই বলেছি। এখন, এখানে আমরা সেই কাজটুকুই করার চেষ্টা করব।
মানে ধরুন, পৃথিবীতে মহাকর্ষ, আমরা যাকে অভিকর্ষ বলি, কীভাবে কাজ করে, সেটা আমরা জানি। কোনো কিছুকে ওপর থেকে ছেড়ে দিলে সেটা তো নিচে পড়ে। এ সময় সে যে টান অনুভব করে, তার মান দূরত্বের বর্গের ব্যস্তানুপাতিক। কিন্তু পৃথিবীর বাইরের কোনো বস্তুর জন্যেও কি মহাকর্ষ এভাবেই কাজ করে? যেমন, চাঁদের জন্য? যদি কাজ করে থাকে, তার মানে চাঁদও পৃথিবীর দিকে পড়ার কথা। এবার একটু থামুন। ভেবে দেখুন তো, চাঁদ কি আসলেই পৃথিবীর দিকে পড়ে? এই টানের মানও কি দূরত্বের বর্গের ব্যস্তানুপাতিক?
এটা বোঝার জন্য ব্যাপারটা একটু ভিন্নভাবে ভেবে দেখা যাক। স্থিরাবস্থা থেকে পৃথিবী পৃষ্ঠের কোনো বস্তুকে নিচের দিকে ছেড়ে দিলে তা যদি প্রথম সেকেন্ডে ১৬ ফুট নিচে পড়ে, একই সময়ে চাঁদ কতটুকু পড়বে?
এই জায়গায় এসে আমরা হয়তো বলব, চাঁদ তো পড়ে না। চাঁদের উপরে যদি কোনো বল কাজ না করত, সে একটা সরলরেখা বরাবর চলে যেত। কিন্তু চাঁদ বৃত্তাকার পথে ঘোরে। তার মানে, বল না থাকলে সরলরেখার যে বিন্দুতে সে থাকত, সেখান থেকে সে সরে এসেছে বা পড়ে গেছে। চাঁদের কক্ষপথের ব্যাসার্ধ (প্রায় ২,৪০,০০০ মাইলের মতো) এবং পৃথিবীর চারপাশে একবার ঘুরে আসতে এর যে সময় লাগে (প্রায় ২৯ দিনের মতো), তা থেকে চাঁদ এক সেকেন্ডে কক্ষপথের ওপর কতটুকু দূরত্ব পাড়ি দেয়, তা আমরা হিসেব করতে পারি। এ থেকে এক সেকেন্ডে তার কতটুকু পতন হয়, সেটা হিসেব করে বের করা যায়। (সেজন্য এক সেকেন্ড আগে চাঁদ তার কক্ষপথের যে বিন্দুতে ছিল, সে বিন্দুতে একটা স্পর্শক আঁকতে হয়। তারপর, বর্তমানে সে যে বিন্দুতে আছে, সে বিন্দুটি স্পর্শকের কতটুকু নিচে, সেই দূরত্বটি বের করতে হয়। এটুকু দূরত্বই সে সরে এসেছে।)
দেখা যায়, এই দূরত্বের মান সেকেন্ডে প্রায় ১/২০ ইঞ্চির মতো। দূরত্বের ব্যস্তানুপাতিক সূত্রের সঙ্গে এটি খাপ খেয়ে যায়। কারণ, পৃথিবীর ব্যাসার্ধ ৪,০০০ মাইল। পৃথিবীর কেন্দ্র থেকে ৪,০০০ মাইলের মতো দূরের কিছু যদি সেকেন্ডে ১৬ ফুট নিচে পড়ে; ২,৪০,০০০ মাইল, মানে আরো প্রায় ৬০ গুণ দূরের কিছু একটার তাহলে সেকেন্ডে ১৬ ফুটের ১/৩৬০০ অংশ পরিমাণ নিচে পড়ার কথা, যেটা ঐ ১/২০ ইঞ্চির মতোই হয়।
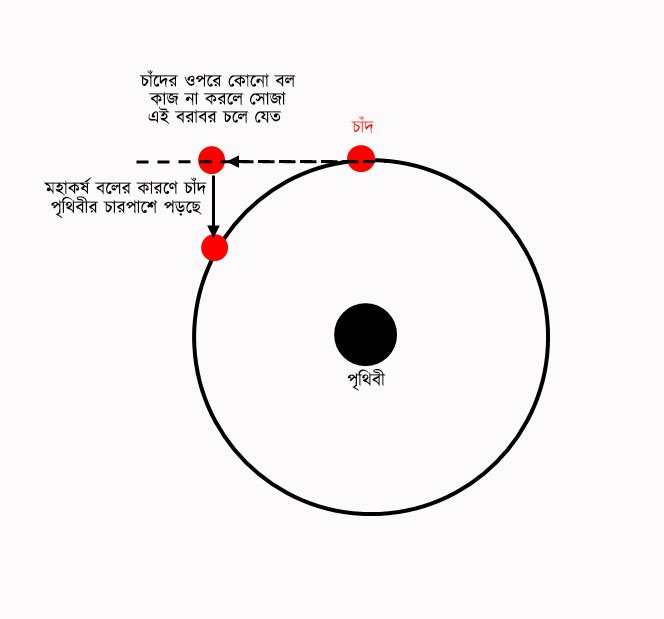
নিউটনও মহাকর্ষ তত্ত্বকে এরকমই একটি হিসেব কষে পরীক্ষা করে দেখতে চেয়েছিলেন। কিন্তু বেশ যত্ন করে, খুঁটিয়ে হিসেব করতে গিয়ে তিনি এত বিশাল অমিল পেলেন যে, তিনি ভাবলেন, তথ্য-উপাত্ত মহাকর্ষ তত্ত্বকে সমর্থন করছে না। তিনি এই ফলাফল আর তখন প্রকাশই করেননি। ছয় বছর পরে এসে জ্যোতির্বিদরা যখন পৃথিবীর আকার নিয়ে নতুন করে মাপজোখ করলেন, দেখা গেল, তারা পৃথিবী থেকে চাঁদের দূরত্ব এতদিন ভুল হিসেব করছিলেন। এটা শোনার পর নিউটন আবার হিসেব কষতে বসলেন। সঠিক দূরত্ব বসিয়ে হিসেব করতেই সব কিছু একেবারে খাপে খাপে মিলে গেল।
চাঁদ যে নিচে পড়ে- এই ধারণাটা বেশ বিভ্রান্তিকর। কারণ, আমরা এটাকে একটুও কাছে আসতে দেখি না। আসলে এই ধারণাটা এত চমৎকার যে, এটাকে আরো কিছুটা ব্যাখ্যা করা প্রয়োজন। মূল কথাটা হলো, চাঁদ নিচে পড়ে মানে- কোনো বল প্রয়োগ না করলে এটা যে সরল রেখা বরাবর চলতে থাকত, সেখান থেকে সে কিছুটা নিচে পড়ে বা সরে আসে।
পৃথিবীপৃষ্ঠে এরকম একটা উদাহরণের কথা ভাবা যাক। পৃথিবীপৃষ্ঠের কাছাকাছি উচ্চতা থেকে কোনো কিছুকে নিচের দিকে ছেড়ে দিলে সেটা প্রথম সেকেন্ডে ১৬ ফুট নিচে পড়বে। এখন, আনুভূমিকভাবে কোনো বস্তুকে যদি ছুঁড়ে মারা হয়, সেটাও কিন্তু প্রথম সেকেন্ডে ১৬ ফুটই পড়বে। যদিও জিনিসটা আনুভূমিকভাবে যাচ্ছে, তারপরও একই সময়ে তার পতন সেই ১৬ ফুটই হবে।
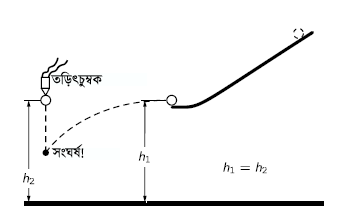
ওপরের ছবিতে একটি যন্ত্র দেখানো হয়েছে, যেটা এই কাজ করে দেখাতে পারে। এখানে, আনুভূমিক ট্র্যাকে একটা বল রাখা আছে, যেটাকে কিছুটা সামনের দিকে ঠেলে দেয়া হবে। আবার একই উচ্চতায় আরেকটি বল রাখা আছে, যেটা নিচের দিকে পড়বে। একটা বৈদ্যুতিক সুইচকে এমনভাবে রাখা হয়েছে, যাতে প্রথম বলটি আনুভূমিক ট্র্যাক ছেড়ে গেলেই দ্বিতীয় বলটি পড়তে শুরু করে। তারা যে সমান সময়ে সমান উচ্চতা পাড়ি দেয়, সেটা মাঝপথে, বাতাসেই তাদের ধাক্কা খাওয়া থেকে দেখা যাবে। বুলেটের মতো প্রবল গতিশীল কোনো বস্তুকেও যদি আনুভূমিকভাবে ছুঁড়ে মারা হয়, এক সেকেন্ডে আনুভূমিকভাবে সে হয়তো দীর্ঘপথ- প্রায় ২,০০০ ফুটের মতো দূরত্ব অতিক্রম করবে। কিন্তু এই পথ যেতে যেতে তার পতন হবে সেই ১৬ ফুটই। আমরা যদি বুলেটটাকে আরো, আরো বেশি দ্রুতবেগে ছুঁড়ে দেই, তাহলে কী হবে?
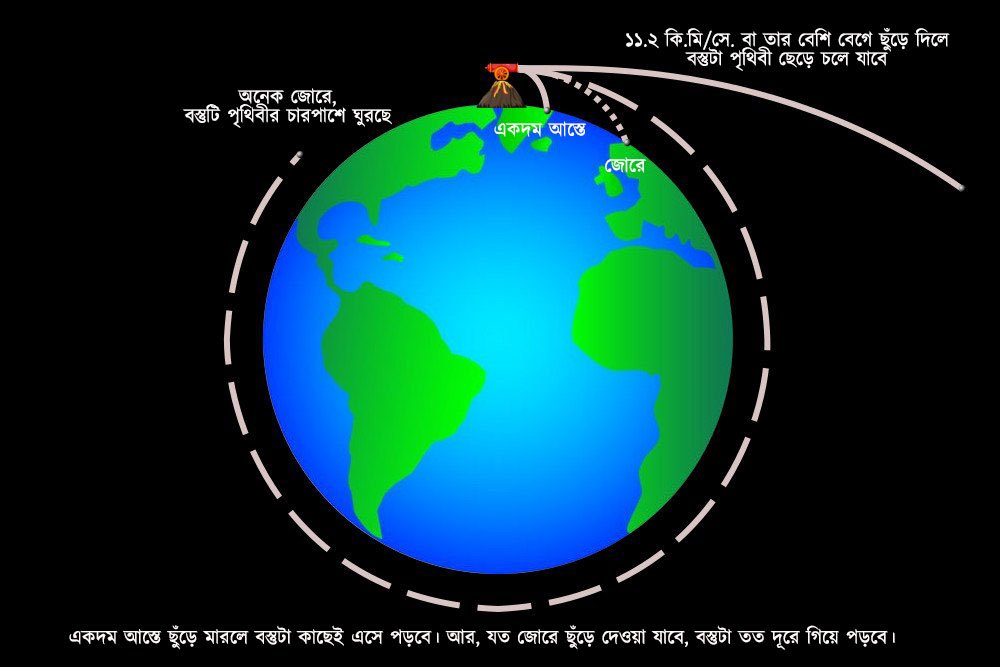
মনে রাখতে হবে, পৃথিবীপৃষ্ঠ আসলে বাঁকানো। ফলে, আমরা বুলেটটিকে অনেক দ্রুত ছুঁড়ে দিলে, সেকেন্ডে ১৬ ফুট নেমে এলেও সেটা কিন্তু পৃথিবীপৃষ্ঠ থেকে আগের সেই উচ্চতাতেই থেকে যেতে পারে। এটা কীভাবে সম্ভব?
আসলে, বুলেটটা পড়ছে ঠিকই, কিন্তু পৃথিবীও বেঁকে যাচ্ছে। ফলে, বুলেটটা আসলে সরাসরি পৃথিবীর দিকে পড়ছে না, বরং পৃথিবীর ‘চারপাশে’ পড়ছে। কথা হলো, সেকেন্ডে ঠিক কতটা দূরত্ব পাড়ি দিলে পরে পৃথিবীপৃষ্ঠ বুলেটের সেই ১৬ ফুট নিচেই থাকবে?
হিসেব করলে দেখা যায়, বুলেটটি যদি সেকেন্ডে ৫ মাইল দূরত্ব পাড়ি দেয়, তাহলে এটা পৃথিবীর দিকে প্রতি সেকেন্ডে ১৬ ফুট করে পড়বে ঠিকই, কিন্তু পৃথিবীপৃষ্ঠ থেকে উচ্চতা হিসেব করলে দেখা যাবে, এটি সেই আগের মতো ১৬ ফুট উপরেই আছে। একটুও কাছে আসেনি। কারণ, এটি পড়ার সাথে সাথে পৃথিবীপৃষ্ঠও প্রতি মুহুর্তে বেঁকে গিয়ে দূরে সরে যাচ্ছিল।
এর মাধ্যমে নিউটন দেখালেন, পৃথিবীতে কোনো কিছু যেভাবে পড়ে, পৃথিবীর বাইরের সবকিছুও সেভাবে পৃথিবীর দিকে পড়ে। কিন্তু গতিবেগ অনেক বেশি হলে বস্তুটা সরাসরি পৃথিবীর ওপরে না পড়ে, এর ‘চারপাশে’ পড়বে।
এর মানে তাহলে কী দাঁড়াল? আসলে, মহাকর্ষ তত্ত্বের ভৌত গুরুত্ব থেকে আমরা বুঝতে পারি, পৃথিবীর বাইরের মহাজাগতিক বস্তু, যেমন- চাঁদ, আমাদের জন্য একদম অচেনা কিছু না। এরাও আসলে আমাদের জানা এই সূত্র মেনেই চলে।
মহাকর্ষ তত্ত্বের আরেকটা গুরুত্বপূর্ণ ব্যাপার হলো, এ থেকে গ্রহগুলোর (আসলে, সব বস্তুর জন্যই) মুক্তিবেগ হিসেব করে বের করা যায়। মুক্তিবেগ মানে, কতটা বেগে একটা কিছুকে (পড়ুন, রকেট) ছুঁড়ে দিলে সেটা আরেকটি বস্তুর (পড়ুন, পৃথিবীর) আকর্ষণ ছিন্ন করে বেরিয়ে যেতে পারবে। সূত্রটাও বেশ সহজ। মুক্তিবেগ, V = √(2GM/R)। এখানে M হলো বস্তুর ভর, আর R সেই বস্তুর ব্যসার্ধ। G হলো বিখ্যাত সার্বজনীন মহাকর্ষীয় ধ্রুবক। সার্বজনীন মানে, পৃথিবীর ভেতরে-বাইরে, মহাকাশে বা মহাবিশ্বের সুদূর কোনো জায়গাতেও এর মান একই থাকে। 6.673 × 10-11 নিউটন-মিটার২/কেজি২।
সবই ঠিক আছে। কিন্তু বস্তুর গতির ব্যাপারে না জানলে, মহাকর্ষ সূত্রকে কাজে লাগানোর তো কোনো উপায় নেই। নাকি? বস্তুর গতি-প্রকৃতি নিয়েও তিনটি সূত্র আবিষ্কার করেছিলেন নিউটন। এরা ‘গতির সূত্র’ নামে খ্যাত।
এই সূত্রগুলোও কিন্তু বেশ সহজ। ঠিক বইয়ের ভাষায় নয়, একটু সহজ কথায় তিনটা সূত্রকে এক নজর দেখে নেয়া যাক।
প্রথম সূত্র: বাইরে থেকে কোনো বল না দিলে যে বস্তু স্থির ছিল, সেটা স্থির থাকবে। আর, যে বস্তু চলছিল, সেটা যে বেগে যেদিকে চলছিল- সেই বেগে, সেদিকেই চলতে থাকবে।
দ্বিতীয় সূত্র: আর যদি বাইরে থেকে বল দেওয়া হয়, তাহলে কী হবে? কোনো বস্তুর ভর আর বেগের গুণফলকে বিজ্ঞানীরা বলেন ভর বেগ। তো, যেদিকে বল দেওয়া হবে, বস্তুটার ভরবেগও সেদিকমুখী হয়ে বদলে যাবে। আর, বল যে হারে দেওয়া হবে, ভরবেগের পরিবর্তনও হবে সেই হারে।
তৃতীয় সূত্র: প্রত্যেক ক্রিয়ার সমান ও বিপরীত প্রতিক্রিয়া আছে। (এটা সম্ভবত সবচেয়ে বিখ্যাত সূত্র!)
এই সূত্রগুলো দিয়েই কিন্তু যেকোনো কিছুর গতিকে ব্যাখ্যা করা যায়। তার মানে, রকেট বিজ্ঞানের মূল কাজগুলো করেছিলেন নিউটন। তবে গ্যালিলিওর অবদানও আসলে কম না। প্রজেক্টাইল বা প্রাসের গতি নিয়ে কাজ করেছিলেন তিনি। দেখিয়েছিলেন, প্রাসের গতি আসলে প্যারাবোলিক বা উপবৃত্তাকার।
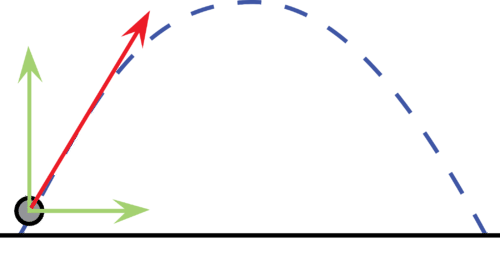
এখন কথা হলো, প্রাস কী? কোনো কিছুকে কোণাকুণিভাবে ওপরের দিকে ছুঁড়ে দিলে, বস্তুটা যে বেগে ছুট দেবে সেই বেগের দুটো অংশ থাকে। একটা অংশ ওপরে-নিচে বরাবর কাজ করে। এর ফলে বস্তুটা নির্দিষ্ট উচ্চতায় উঠতে পারে। আবার, বেগের আরেকটা অংশ কাজ করে পাশাপাশি। এর ফলে বস্তুটা নির্দিষ্ট দূরত্ব অতিক্রম করে, যেখান থেকে ছুঁড়ে দেওয়া হয়েছে তার কিছুটা দূরে গিয়ে পড়ে। তো, এভাবে কোণাকুণি ছুঁড়ে দেওয়া যেকোনো কিছুই আসলে প্রাস বা প্রজেক্টাইল।
রকেট থেকে শুরু করে বুলেট পর্যন্ত সবকিছুই গ্যালিলিওর এই সূত্র মেনেই কাজ করে। তবে প্রাসের গতির সূত্র নিয়ে কাজ করলেও, বস্তুর অন্য ধরনের গতি নিয়ে তেমন কিছু করে যাননি গ্যালিলিও। সহজ কথায়, নিউটনের গতি ও মহাকর্ষ সূত্র ছাড়া, শুধু গ্যালিলিওর সূত্রগুলোর ওপরে ভিত্তি করে রকেট বিজ্ঞান গড়ে উঠতে পারত না। সেজন্য গ্যালিলিওকে নয়, নিউটনকেই রকেট বিজ্ঞানের মূল কারিগর হিসেবে স্বীকার করে নেওয়া হয়েছে।
নিউটন তো শুধু মৌলিক তত্ত্ব আবিষ্কার করেছিলেন। কিন্তু এই সূত্র ব্যবহার করে পৃথিবীর সীমানা ছাড়িয়ে যাওয়ার স্বপ্ন কখন থেকে দেখতে শুরু করল মানুষ? আসলে, এই স্বপ্ন কিন্তু বিজ্ঞানীরা দেখেননি। দেখেছিলেন এক কল্পবিজ্ঞান লেখক। জুলভার্ন। রকেট ও মানুষের মহাকাশযাত্রার ইতিহাসে যাঁর কথা না বললে সেই ইতিহাস অসম্পূর্ণই থেকে যাবে।
সিরিজটির আগের পর্বগুলো পড়তে ক্লিক করুন: ১ম পর্ব
মহাকাশ সম্বন্ধে আরও জানতে পড়তে পারেন এই বইগুলো:
১) মহাকাশের মহাবিস্ময়
২) মহাকাশে কী ঘটছে
৩) মহাকাশে প্রাণের সন্ধান








